In the realm of geometry, a cube stands as a beacon of simplicity and order. With its sharp edges and congruent faces, it embodies the concept of three-dimensionality. As we venture into the depths of this geometrical figure, let us focus on a 9-inch cube, unraveling the secrets it holds within its cubic dimensions.

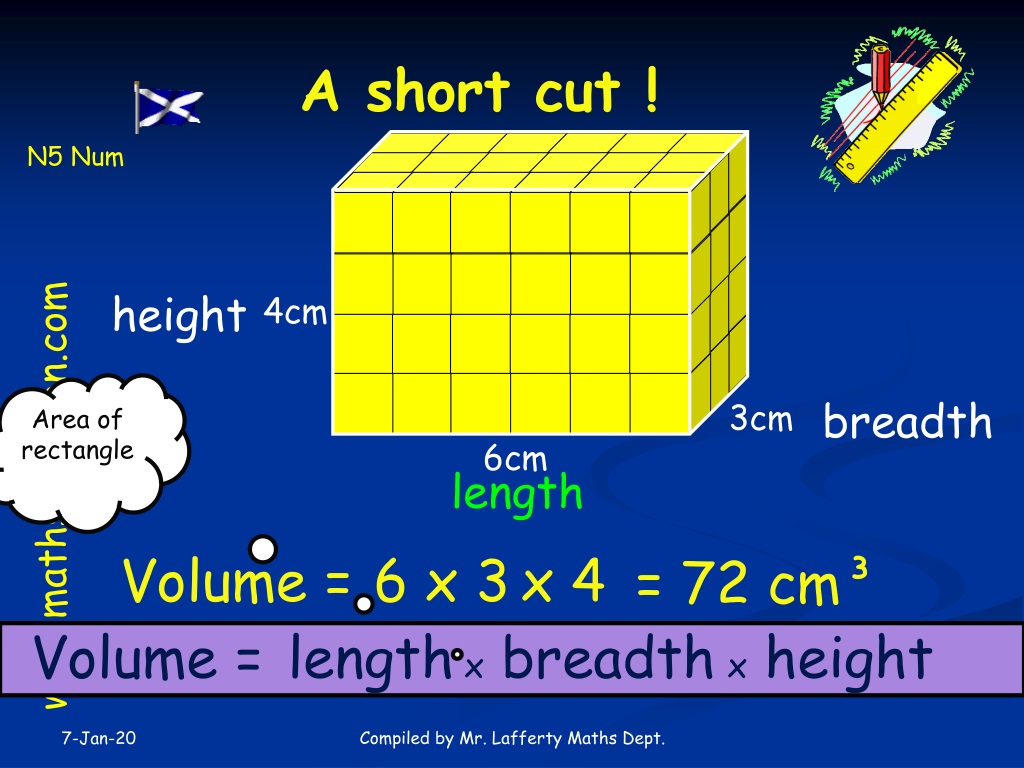
Image: www.slideserve.com

A cube, as defined by mathematics, possesses six square faces, with each side exhibiting equal length. The length of each edge, in the case of a 9-inch cube, measures 9 inches. This uniform measurement across all edges grants the cube its characteristic shape—a perfect square extruded into the third dimension.

Volume: A Cubic Calculation

When we seek to determine the volume of any three-dimensional object, we embark on a journey into the mathematics of space. Volume, by its essence, represents the amount of space an object occupies within the confines of its boundaries. For a cube, with its orthogonal faces, the formula for volume becomes straightforward:

Volume = (Side Length) ^ 3

Substituting the 9-inch value for the side length, we arrive at the volume of our 9-inch cube:

Volume = (9 inches) ^ 3

Volume = 729 cubic inches

Therefore, a 9-inch cube possesses a volume of 729 cubic inches, which essentially signifies the number of cubic inch units it can accommodate. This value serves as a significant measure, enabling us to compare the capacity of different cubes and other three-dimensional objects.

Spatial Reasoning: Unlocking Geometric Dimensions

The concept of volume extends beyond mere calculation; it delves into the realm of spatial reasoning, where we develop an intuitive understanding of the world around us. By grasping the volume of a 9-inch cube, we cultivate an appreciation for the spatial relationships between objects.

Consider two cubes: one with a side length of 9 inches and the other, half its size, with a side length of 4.5 inches. Despite their differing sizes, they share a commonality: their volumes are proportional to the cube of their side lengths. This observation reinforces the fundamental principle that the volume of a cube is not merely a product of its dimensions but a cubic function, intricately linked to the three-dimensional nature of its form.

Applications in Everyday Life

The concept of volume, exemplified by our 9-inch cube, finds practical applications in numerous facets of our lives. From understanding the capacity of storage containers to calculating the space required for a room, volume serves as an indispensable tool in diverse fields.

Architects and interior designers utilize volume calculations to optimize space and create aesthetically pleasing environments. Engineers rely on volume measurements to ensure the structural integrity of bridges and buildings. Chemists and biologists use volume to determine the concentration of solutions and the volume of cells, respectively.

Conclusion: Embracing the Power of Volume

The 9-inch cube, with its volume of 729 cubic inches, offers a tangible representation of volume and spatial reasoning. It exemplifies the significance of understanding three-dimensional objects and their spatial relationships. By exploring the concept of volume, we unlock a wealth of knowledge, empowering us to navigate the world with confidence and precision.

As you encounter cubes and other three-dimensional objects, we encourage you to pause and ponder their volumes. Allow their dimensions to inspire spatial awareness and appreciation for the intricate world of geometry. Volume reigns as a fundamental concept, serving as a cornerstone in diverse disciplines, from architecture to chemistry and beyond. By embracing the power of volume, you open doors to a deeper understanding of the world and a renewed perspective on the objects that populate it.

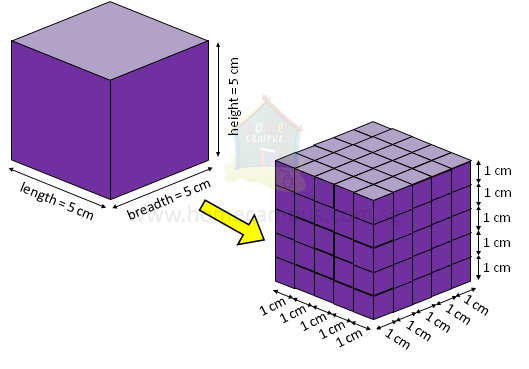
Image: my.homecampus.com.sg

A 9 Inch Cube Has A Volume Of