In the realm of geometry, understanding the surface area of cubes and rectangular prisms holds paramount importance. These shapes permeate our daily lives, from the skyscrapers that grace our cityscapes to the humble boxes that store our belongings. Embarking on a journey into the world of surface area unravels a wealth of practical applications and profound insights into the built environment around us.

Defining Surface Area

At its core, surface area measures the total perimeter of an object’s exterior surfaces. For cubes, which are six-sided, square-shaped figures, the surface area is simply the sum of each face’s area. Rectangular prisms, on the other hand, possess two rectangular bases and four rectangular side walls; thus, their surface area encompasses the areas of all six surfaces.

Formula Explorations

Unveiling the secrets of surface area requires delving into the mathematical formulas that govern these shapes. For cubes, the formula is as follows:

Surface Area = 6 s^2

where ‘s’ represents the length of each side.

For rectangular prisms, the formula becomes slightly more complex:

Surface Area = 2 (lw + hw + lh)

where ‘l’ denotes the length, ‘w’ the width, and ‘h’ the height of the prism.

Applications in Our World

The significance of surface area extends far beyond the classroom. In architecture, meticulous surface area calculations ensure optimal insulation against the elements, preserving indoor climate regulation and energy efficiency. For packaging designers, understanding surface area enables precise estimation of material needs, minimizing waste and enhancing product presentation.

Expert Insights

“Surface area is an essential parameter in many engineering applications,” explains Dr. Martha Rogers, an acclaimed structural engineer. “When designing bridges, for instance, we need to determine the surface area of the bridge deck to calculate its resistance to wind and gravity forces.”

Practical Tips for Calculation

• Familiarize yourself with the formulas for both cubes and rectangular prisms.

• Accurately measure the length, width, and height of the shape using a ruler or measuring tape.

• Substitute the measurements into the appropriate formula and evaluate the result.

Conclusion

Mastering the surface area of cubes and rectangular prisms equips individuals with a powerful tool to solve problems and gain insights into the world around them. Whether you’re navigating the complexities of construction, optimizing packaging design, or simply seeking to understand the fundamentals of geometry, a thorough grasp of surface area will illuminate your path. In the pursuit of knowledge, may this guide serve as a beacon, illuminating your understanding of these enigmatic shapes.

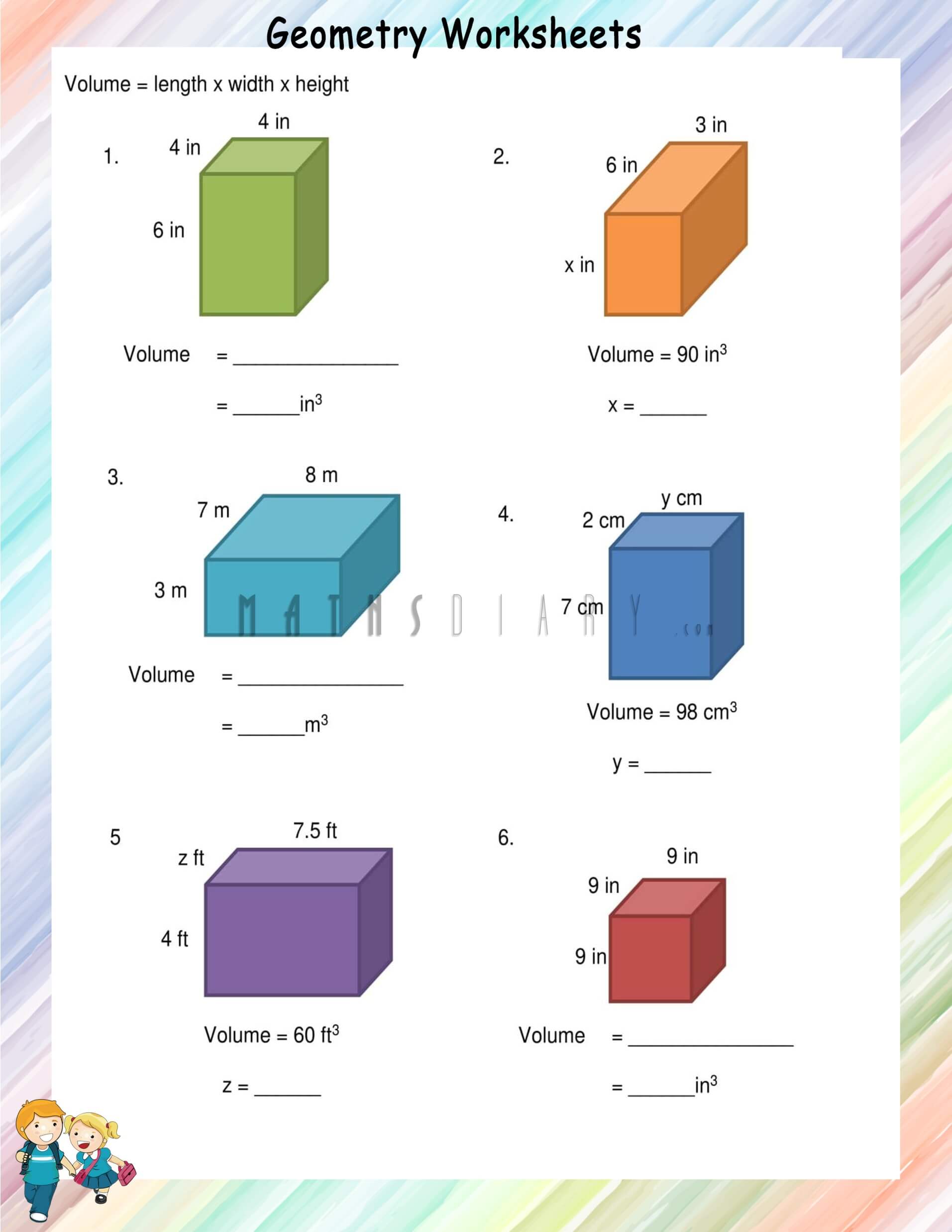
Image: www.mathsdiary.com

Surface Area Of Cubes And Rectangular Prisms