In the realm of geometry, understanding the intricacies of angles is paramount. One of the most fundamental concepts in this field is the Angle Sum Theorem, which unravels the mystery behind the sum of interior angles in a triangle. Join us on an expedition to explore this theorem, its history, and its profound implications.

Image: www.wikihow.com
The Angle Sum Theorem: A Cornerstone of Geometry
The Angle Sum Theorem postulates that the sum of the interior angles of any triangle is always equal to 180 degrees. This extraordinary theorem holds true for all triangles, regardless of their shape or size. The theorem, attributed to the ancient Greek mathematician Euclid, has served as a cornerstone of geometry for centuries.
A Geometric Trek: Visualizing the Theorem
To grasp the essence of the Angle Sum Theorem, embark on a geometric adventure. Begin with any arbitrary triangle. Using a protractor, meticulously measure each of its three interior angles. Sum these angles, and behold the remarkable outcome: the sum will invariably equal 180 degrees. This holds true for acute triangles, where all angles are less than 90 degrees, right triangles, where one angle is 90 degrees, and even obtuse triangles, where one angle exceeds 90 degrees.
A Historical Odyssey: Tracing the Theorem’s Origins
The Angle Sum Theorem’s roots extend far back into the annals of mathematical exploration. Its earliest known formulation can be traced to Euclid’s “Elements,” a seminal work of geometry composed around 300 B.C. Euclid’s rigorous axiomatic approach established the theorem as a fundamental pillar of geometric knowledge.
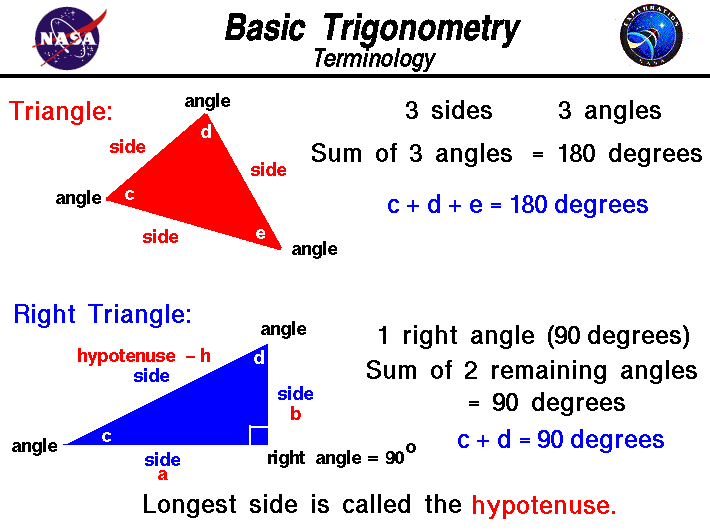
Image: trigonometri-logaritma.blogspot.com
Delving into Euclid’s Proof: A Triumph of Logic
Euclid’s proof of the Angle Sum Theorem is a masterful display of logical reasoning. It begins with the dissection of a triangle into a pair of triangles by drawing a line parallel to any of its sides. Euclid then demonstrates that the sum of the angles in the newly formed triangles equals 180 degrees. By skillfully extending this logic to the original triangle, Euclid elegantly establishes the theorem’s validity.
Practical Applications: Unleashing the Power of Geometry
The Angle Sum Theorem is an indispensable tool in a vast array of real-world applications. Architects, engineers, and designers rely on it to ensure the structural integrity of buildings, bridges, and other constructions. Surveyors harness its power to map land boundaries accurately, while astronomers employ it to determine the positions of celestial bodies.
Unveiling the Mystery of Triangles: A Journey of Discovery
Through meticulous experimentation and rigorous mathematical proofs, scholars have unraveled the secrets of triangles. The Angle Sum Theorem serves as a testament to the power of human curiosity and the enduring value of geometry. As you delve deeper into this captivating field, you will embark on a journey of discovery that will ignite your intellect and broaden your understanding of the world around you.
How Many Degrees Are There In A Triangle
FAQs: Illuminating the Angle Sum Theorem
- Q: How can I calculate the sum of the interior angles of a triangle?
A: Use a protractor to measure each of the three angles and then add the measurements together.
- Q: Is the Angle Sum Theorem true for all triangles, regardless of their shape or size?
A: Yes, the Angle Sum Theorem holds true for all triangles.
- Q: Who first discovered the Angle Sum Theorem?
A: The Angle Sum Theorem is attributed to the ancient Greek mathematician Euclid.
- Q: What are some practical applications of the Angle Sum Theorem?
A: The Angle Sum Theorem is used in architecture, engineering, design, surveying, and astronomy.
Are you ready to dive deeper into the fascinating world of triangles and unlock their geometric secrets? Join us on an exploration of the Angle Sum Theorem and its profound implications.