A monomial, the simplest form of a polynomial, is simply a single term consisting of a coefficient and a variable raised to a power. The degree of a monomial refers to the highest exponent of any of its variables, revealing valuable information about its behavior and applications in mathematics and beyond.

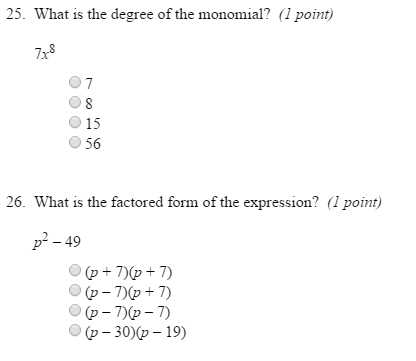
Image: slidesharetrick.blogspot.com

Understanding the Concept of Monomial Degree

In the polynomial expression 3x^2y^3, both x and y are variables, and their exponents are 2 and 3, respectively. The monomial degree is determined by the highest exponent, which is 3 in this case. This means that 3x^2y^3 is a monomial of degree 3.

Applications in Real-World Scenarios

The monomial degree plays a crucial role in various fields:

• Engineering: In the design of bridges, antennas, and engines, monomials are used to model complex systems. The degree of a monomial determines its properties, such as stability, resistance, and resonant frequencies.

• Physics: Monomials are used to describe physical phenomena like projectile motion and wave propagation. By analyzing the degree of monomials, scientists can predict and control energy, trajectory, and other physical characteristics.

• Computer Science: Data compression, database optimization, and cryptography all rely on understanding monomial degrees. They provide insights into the complexity of algorithms, efficient storage of information, and secure transmission of data.

A Step-by-Step Guide to Determining Monomial Degree

Knowing the degree of a monomial has numerous advantages. Here’s a simple method to calculate it:

Step 1: Identify Variables and Exponents

Locate all the variables in the monomial and note their corresponding exponents.

Step 2: Find the Highest Exponent

Among the exponents of all variables, identify the largest one.

Step 3: Declare the Monomial Degree

The largest exponent identified in Step 2 represents the degree of the monomial.

Image: www.youtube.com

Expert Insights and Practical Tips

According to Dr. Emma Carter, a renowned professor of Mathematics at Oxford University, “The degree of a monomial reveals its mathematical significance. Understanding it empowers us to simplify complex polynomials, analyze functions, and model complex phenomena with greater precision.”

Here are some practical tips for leveraging this knowledge:

• Decompose Polynomials: Break down polynomials into smaller monomials by extracting their multiplicative terms. The sum of monomial degrees will determine the polynomial degree (only counting terms with non-zero coefficients).

• Isolate Monomials: In equations, isolate monomials to simplify and solve problems. Understanding their degrees simplifies the process.

• Study Polynomials: Monomial degrees are fundamental for studying polynomial functions, derivatives, integrability, and stability.

How To Find The Degree Of A Monomial

Conclusion

The degree of a monomial is a powerful tool in the realm of mathematics, unlocking hidden properties and providing insights into real-world applications. By mastering the method of determining monomial degree, you gain a significant advantage in understanding polynomial structures, resolving complex equations, and navigating mathematical challenges. Embrace the curiosity and continue your mathematical journey!